| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | |||||
| 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| 17 | 18 | 19 | 20 | 21 | 22 | 23 |
| 24 | 25 | 26 | 27 | 28 | 29 | 30 |
- 5585
- 웹케이알
- C언어
- JS
- 딥러닝
- 계단함수
- 코드엔진
- 웹해킹
- Old-17
- Old-14
- 자바스크립트
- c언어 게임
- boj
- 10809
- c++
- 코딩테스트 연습
- openCV
- 프로그래머스
- 게임 프로그래밍
- 신규 아이디 추천
- 크레인 인형뽑기
- 네트워크
- 자바
- old-1
- tcp
- 백준
- webhacking.kr
- 리버싱
- 퍼셉트론
- 소프트맥스 함수
- Today
- Total
SteffenLee
[Deep Learning]신경망 본문
신경망은 기계 학습과 인공지능 분야에서 사용되는 일종의 도구입니다. 사람의 뇌의 작동 방식에서 영감을 받아 만들어진 모델로, 입력 데이터를 처리하고 패턴을 학습하여 문제를 해결하는 능력을 갖추고 있습니다.
신경망의 구조는 기본적으로 입력층과 은닉층, 출력층으로 구성이 되어 있으며 아래 사진과 같은 형태를 지닙니다.

신경망에 대해 자세하게 알아보기 전에 퍼셉트론이라는 개념을 알아야한다.
퍼셉트론은 이전 글에서 설명했으니 참고바랍니다.
https://steffen-lee.tistory.com/65
[Deep Learning]퍼셉트론이란?
퍼셉트론이란? 퍼셉트론은 1957년 프랑크 로젠블라트라는 사람이 고안한 알고리즘입니다. 다수의 신호를 입력받아 하나의 신호로 출력하는데, 여기서 말하는 신호는 전류처럼 흐름이 있는 것을
steffen-lee.tistory.com
활성화 함수
활성화 함수는 말 그대로 입력 신호의 총합이 활성화를 일으키는지 알려주는 함수인데, 퍼셉트론에 내부에서 입력신호를 변환해주는데
사용이 된다.
여기서 변환된 값은 다음 노드(뉴런)으로 전달이 된다.
밑에서 그래프를 보며 설명하겠지만, 활성화 함수에서는 비선형 함수(직선 1개로 표현하지 못하는)를 많이 사용하는데
그 이유는 선형함수를 사용하게 되면 복잡한 네트워크를 표현할 수 없게된다.
예를 들어 일차 함수를 활성화 함수로 사용하게 되면, 3층 네트워크는 3차 함수로 표현이 된다.
다시 말해, 복잡한 네트워크를 표현하지 못한다.
활성화 함수의 종류에는 계단 함수와 시그모이드 함수, ReLU 함수가 있다.
계단 함수는 0이하일 때는 0을 출력하고. 0초과일 때는 1을 출력한다.

다음으로는 또 다른 활성화 함수인 시그모이드 함수이다.
시그모이드 함수는 아래와 같은 수식으로 이루어진다.

exp는 자연상수 e를 밑으로하는 지수함수를 뜻한다.
해당 함수를 코드로 구현하면
def sigmoid(x):
return 1 / (1 + np.exp(-x)) #시그모이드 함수 수식을 통해 구현 exp는 자연상수이렇게 구현할 수 있다.
해당 함수를 통해 그래프를 그리게 되면
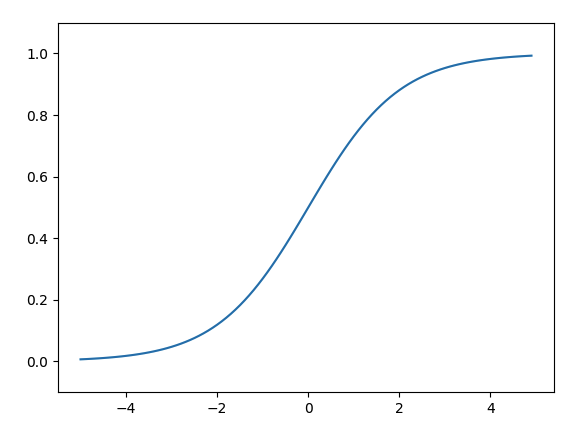
위와 같은 형식의 그래프가 그려지게 됩니다.
계단 함수는 0또는 1의 출력값을 갖는 반면, 시그모이드 함수는 0.11234, 0.6234와 같이 다양한 값을 가집니다.
과거에는 시그모이드 함수를 주로 이용했으나, 최근에는 ReLU함수를 많이 이용합니다.
ReLU함수를 수식으로 표현하면 아래와 같이 표현이 가능합니다.

0이하가 입력되면 0을 반환하고, 0 이상을 입력받으면 그 값을 그대로 반환합니다.
그래프를 그리게 되면 아래와 같이 나옵니다.

ReLU함수를 코드로 구현하면
def relu(x):
return np.maximum(0,x) #두 값을 비교하여 더 큰 값을 반환넘파이의 맥시멈 함수를 이용해 구현이 가능합니다.
출력층의 활성화 함수
신경망에서 분류와 회귀를 사용할 수 있지만, 어느 걸 하느냐에 따라 출력층에서 사용되는 활성화 함수가 달라집니다.
회귀에는 항등 함수, 분류에는 소프트 맥스 함수를 사용합니다.
항등함수는 입력을 그대로 출력한다. 즉, 입출력이 항상 같다는 것이다.
소프트 맥스 함수의 수식은

n은 출력층의 뉴런 수, yk는 그 중 k번째 출력임을 뜻한다. 소프트맥스 함수의 분자는 입력신호 ak의 지수함수, 분모는 모든 입력 신호의
지수합수의 합이다.
위 수식을 코드로 구현하면 다음과 같이 구현할 수 있다.
import numpy as np
#수식을 통한 함수 구현
def softmax(a): #함수 명명 규칙에 따라 코드를 수정
exp_a = np.exp(a) #지수 함수
sumExpA = np.sum(exp_a)
y = exp_a / sumExpA
return y하지만 이 수식에는 문제점이 하나 존재하는데, 바로 수치가 너무 커질 수 있다는 문제가 있다.
가령 ak값이 1000이라면 e^1000이라면 수치가 엄청나게 커지게 된다. 큰 값끼리 나눗셈 연산을 하게 되면 결과 수치가 불안정해진다.
그래서 이 문제를 해결하기 위해 상수 c를 곱해주면 해결이 된다.
수식을 수정해주면 아래와 같이 수정할 수 있다.

소프트 맥수 함수의 특징은 0~1사이의 소수 값으로 출력값이 주어지고, 모든 출력값의 총합은 1이라는 성질이 있다.
이 성질 덕분에 확률로 해석할 수 있다.
감사합니다.
'Artificial Intelligence > Deep Learning' 카테고리의 다른 글
| [Deep Learning]논리 회로 구현(AND, NAND, OR) (0) | 2022.11.30 |
|---|---|
| [Deep Learning]퍼셉트론이란? (0) | 2022.11.29 |


